On Defined by Modulus

N. Subramanian

Abstract


In this paper we defined the 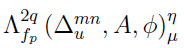      defined by a modulus and exhibit some general properties of the space with an four dimensional infinite regular matrix.


Keywords


Gai sequence; Analytic sequence; Modulus function; Double sequences; Difference sequence; Lacunary sequence; Statistical convergence

Full Text:

PDF

References


REFERENCES

[01] Apostol, T. (1978). Mathematical analysis. London: Addison-Wesley.

[02] Basarir, M., & Solancan, O. (1999). On some double sequence spaces. J. Indian Acad. Math., 21(2), 193-200.

[03] Bektas, C., & Altin, Y. (2003). The sequence space lM (p, q, s) on seminormed spaces. Indian J. Pure Appl. Math., 34(4), 529-534.

[04] Bromwich, T. J. I'A. (1965). An introduction to the theory of infinite series. New York: Macmillan and Co. Ltd.

[05] Hardy, G. H. (1917). On the convergence of certain multiple series (pp.86-95). Proc. Camb. Phil. Soc.

[06] Krasnoselskii, M. A., & Rutickii, Y. B. (1961). Convex functions and orlicz spaces. Netherlands: Gorningen .

[07] Lindenstrauss, J., & Tzafriri, L. (1971). On orlicz sequence spaces. Israel J. Math., 10, 379-390.

[08] Maddox, I. J. (1986). Sequence spaces defined by a modulus. Math. Proc. Cambridge Philos. Soc, 100(1), 161-166.

[09] Moricz, F. (1991). Extentions of the spaces c and c0 from single to double sequences. Acta. Math. Hung., 57(1-2), 129-136.

[10] Moricz, F., & Rhoades, B. E. (1988). Almost convergence of double sequences and strong regularity of summability matrices. Math. Proc. Camb. Phil. Soc., 104, 283-294.

[11] Mursaleen, M. A. K., & Qamaruddin. (1999). Difference sequence spaces defined by Orlicz functions. Demonstratio Math., Vol. XXXII, 145-150.

[12] Nakano, H. (1953). Concave modular. J. Math. Soc. Japan, 5, 29-49.

[13] Orlicz,W. (1936). über Raume (LM). Bull. Int. Acad. Polon. Sci. A, 93-107.

[14]Parashar, S. D., & Choudhary, B. (1994). Sequence spaces defined by Orlicz functions. Indian J. Pure Appl. Math. , 25(4), 419-428.

[15] Rao, K. C., & Subramanian, N. (2004). The Orlicz space of entire sequences. Int. J. Math. Sci., 68, 3755-3764.

[16] Ruckle, W. H. (1973). FK spaces in which the sequence of coordinate vectors is bounded. Canad. J. Math., 25, 973-978.

[17] Tripathy, B. C. (2003). On statistically convergent double sequences. Tamkang J. Math., 34(3), 231-237.

[18] Tripathy, B. C., & Altin, Y. (2003). Generalized difference sequence spaces defferned by Orlicz function in a locally convex space. J. Anal. Appl., 1(3), 175-192.

[19] Turkmenoglu, A. (1999). Matrix transformation between some classes of double sequences. J. Inst. Math. Comp. Sci. Math. Ser., 12(1), 23-31.

[20] Kamthan, P. K., & Gupta, M. (1981). Sequence spaces and series, lecture notes, pure and applied

Mathematics. New York: 65 Marcel Dekker, In c.

[21] Gǒkhan, A., & Colak, A. (2004). The double sequence spaces cP2 (p) and cPB2 (p). Appl. Math. Comput.,157(2), 491-501.

[22] Gǒkhan, A., & Colak, A. (2005). Double sequence spaces l∞2 . ibid., 160(1), 147-153.

[23] Zeltser, M. (2001). Investigation of double sequence spaces by soft and hard analitical methods. Dissertationes Mathematicae Universitatis Tartuensis 25, Tartu University Press, Univ. of Tartu, Faculty of Mathematics and Computer Science, Tartu.

[24] Mursaleen, M., & Edely, O. H. H. (2003). Statistical convergence of double sequences. J. Math. Anal. Appl., 288(1), 223-231.

[25] Mursaleen, M. (2004). Almost strongly regular matrices and a core theorem for double sequences. J. Math. Anal. Appl., 293(2), 523-531.

[26] Mursaleen, M., & Edely, O. H. H. Almost convergence and a core theorem for double sequences. J. Math. Anal. Appl., 293(2), 532-540.

[27] Altay, B., & BaSar, F. (2005). Some new spaces of double sequences. J. Math. Anal. Appl., 309(1), 70-90.

[28] BaSar, F., & Y.Sever, Y. (2009). The space Lp of double sequences. Math. J. Okayama Univ, 51, 149-157.

[29] Subramanian, N., & Misra, U. K. (2010). The semi normed space de_ned by a double gai sequence of modulus function. Fasciculi Math., 46.

[30] H.Kizmaz, H. (1981). On certain sequence spaces. Cand. Math. Bull., 24(2), 169-176.

[31] Kuttner, B. (1946). Note on strong summabilit. J. London Math. Soc., 21, 118-122.

[32] Maddox, I. J. (1979). On strong almost convergence. Math. Proc. Cambridge Philos. Soc., 85(2), 345-350.

[33] Cannor, J. (1989). On strong matrix summability with respect to a modulus and statistical convergence. Canad. Math. Bull., 32(2), 194-198.

[34] Pringsheim, A. (1900). Zurtheorie derzweifach unendlichen zahlenfolgen. Math. Ann., 53, 289-

321.

[35] Hamilton, H. J. (1936). Transformations of multiple sequences. Duke Math. J., 2, 29-60.

[36] Hamilton, H .J. (1930). A Generalization of multiple sequences transformation. Duke Math. J., 4, 343-358.

[37] Hamilton, H. J. (1938). Change of Dimension in sequence transformatio , Duke Math. J., 4, 341-342.

[38] Hamilton, H. J. (1939). Preservation of partial Limits in Multiple sequence transformations. Duke Math. J.,4, 293-297.

[39] Robison, G. M. (1926). Divergent double sequences and series. Amer. Math. Soc. Trans., 28, 50-73.

[40] Silverman, L. L. (xxx). On the definition of the sum of a divergent series, un published thesis. University of Missouri studies, Mathematics series.

[41] Toeplitz, O. (1911). über allgenmeine linear mittel bridungen. Prace Matemalyczno Fizyczne (warsaw), 22.

[42] BaSar, F., & Atlay, B. (2003). On the space of sequences of p- bounded variation and related matrix mappings. Ukrainian Math. J., 55(1), 136-147.

[43] Altay, B., & BaSar, F. (2007). The fine spectrum and the matrix domain of the difference operator △ on the sequence space lp; (0 < p < 1), Commun. Math. Anal., 2(2), 1-11.

[44] Colak, M.Et R., & E.Malkowsky, E. (2004). Some topics of sequence spaces, lecture notes in mathematics (pp.1-63). Firat Univ. Elazig, Turkey, Firat Univ. Press, ISBN: 975-394-0386-6.




DOI: http://dx.doi.org/10.3968/5450

DOI (PDF): http://dx.doi.org/10.3968/g6169

Refbacks

  • There are currently no refbacks.


Copyright (c)



Share us to:   

Reminder

If you have already registered in Journal A and plan to submit article(s) to Journal B, please click the CATEGORIES, or JOURNALS A-Z on the right side of the "HOME".


We only use three mailboxes as follows to deal with issues about paper acceptance, payment and submission of electronic versions of our journals to databases:
caooc@hotmail.com; sms@cscanada.net; sms@cscanada.org

 Articles published in Studies in Mathematical Sciences are licensed under Creative Commons Attribution 4.0 (CC-BY).

 STUDIES IN MATHEMATICAL SCIENCES Editorial Office

Address: 1055 Rue Lucien-L'Allier, Unit #772, Montreal, QC H3G 3C4, Canada.

Telephone: 1-514-558 6138

Http://www.cscanada.net
Http://www.cscanada.org
E-mail:caooc@hotmail.com

Copyright © 2010 Canadian Research & Development Centre of Sciences and Cultures